< Raytracing

< IBL and HDRI

> Intro

> Overview

• Correction

> HDRI and Gamma

— IBL and HDRI: HDRI for IBL, Correction —

Correct and remap panoramas

The most suitable projection to correct a panorama is that with the names «Spherical», «Equirectangular» and «Latitude/Longitude». In this rectangular projection, each square degree has the same area – whether it is at a pol or at the equator. The picture of such a projection is double as wide than high: 360° horizontal, 180° vertical.

If you want to put a picture material on a sphere in Bryce, this would be the projection to use. The picture will be mapped perfectly onto the sphere.

Cubical Panorama.

The picture shows the spherical projection of the panorama made from the six faces of a cube. It is flawless. Each of the 30° by 30° squares have the same size.

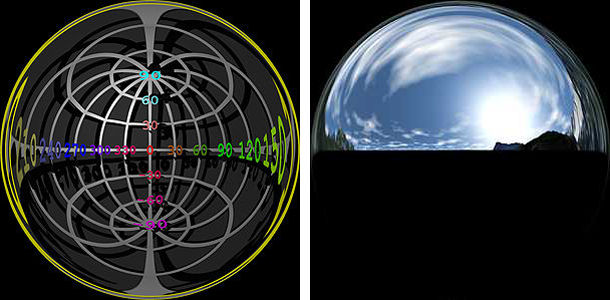
Mirror Ball

All four renders from the mirror ball were transformed into the spherical projection. They are mirrored and show considerable distortions at the sides. The black dot is grey, yellow or blue because the square part to the perimeter of the disk was not set to black with an object mask.

The blind (or black) dot is divided and the parts are visible at left and at right. Consider the increasing degree of distortion towards the left and right edges.

Flaws in the picture are more conveniently corrected in the spherical projection than in that of a mirror ball.

From the best and least distorted parts, a new panorama was constructed. In the same manner, camera and photographer would be removed. The panorama is undistorted and in the same quality as the one made from the six cube faces.

Using a graphics program, the best parts of the pictures were copied and assembled seamessly into a completely new picture. Only three views were needed: from front, left and right. The view from the back side was not used to create the new panorama. Finally, the picture was mirrored.

Sky Dome

The pictures below show the panorama created using a mirror ball rendered from above. If such a panorama is transformed, you get what is shown at left. If the panorama is tilted back into horizontal, the picture shown at right results.

A skydome panorama should look like photographed using a fisheye lens looking in the sky. Everything below the horizon must be removed.

In a graphics program, the lower half of the picture was set to black.

This is now the correct panorama from a skydome in the spherical projection.

Panorama Projection for Bryce 6 IBL

The Bryce 6 raytracing program expects the HDRI panoramas for IBL in the «Angular Map» — also called «Light Probe» — projection. Bryce 7 can additionally handle spherical panoramas as well. The angular map projection might look the same like the mirror ball to the causal observer. However, a closer look reveils that the «longitude» lines have the same distance to each other, something that is not the case on a mirror ball.

At left the cage in the final projection, at right the sky dome. In the spherical projection the pols become lines; in the angular projection, what is behind is put on the edge of the sphere as a ring around the disk.

This concludes the creation of a panorama. For an HDRI, many such panoramas with different light intensities are needed.

The size for a panorama

If a scene is lit by an image (IBL), the panorama can be rendered as backdrop. This is not mandatory for the lighting effects, but could enhance the appearance of the scene. Such panoramas in the background are often blurred. This can be an advantage if it is intended that the beholder concentrates on the sharp foreground object depicted. If the backdrop were crisp and well focused, the option render with depth of field (DOF) would have to be engaged with the known penalty of grossly increased render time.

Spherical panoramas can also be mapped on the inside of a ball which surrounds the scene. Such panoramas can be made with conventional pictures; HDRI is not needed if it is not the intention to light the scene by IBL. A blurred appearance could be an advantage in this case, too. Imagine a render of a racing car with a motion blurred background.

But what, if the backdrop has to be well focused? Then, a very large panorama must be applied. How large can be estimated by the following.

Ypano = 180° / AOFy • Yrender

Xpano = 2 • Ypano

 

Ypano	=	Height in pixels of the panorama in spherical projection,
Yrender	=	Height in pixels of the rendered picture,
AOFy	=	Vertical angle of field of the camera in degrees in the rendered picture,
Xpano	=	Width in pixel of the panorama in spherical projection.

Example 1:
What size is needed for a panorama in spherical projection if the vertical angle of view of the camera is 30° and the finished picture 800 pixels high?

180° / 30° x 800 px = 4,800 px vertical; x 2 = 9,600 px horizontal.

The mirror ball must have a diameter of 7,660 pixels to have the same surface as the panorama in the latitude/longitude projection.

Example 2:
We have got a «Light Probe» in the Angular Map projection which has a diameter of 1,600 pixels. In what height may the picture be rendered to get a focused background if the vertical angle of field of the camera is set to 45°?

The surface of the disk with 1,600 pixels diameter is calculated first:

(1,600 px / 2)^2 x pi = 2,010,618 Pixel.

Since the spherical projection is twice as wide as it is high, the result is divided by 2 and from this the square root is taken. Thus, the height is determined:

SQRT(2,010,618 px / 2) = 1,003 pixels.

By rearranging the formula above, the answer is optained:

1,003 px x 45° / 180° = 251 pixels.

If this light probe is used and the camera's vertical angle of field is set to 45°, the final picture may be rendered with a height of just 250 pixels in order to have the backdrop appear well focused.

Example 3:
We have got a «Light Probe» in the Angular Map projection which has a diameter of 1,600 pixels. To what angle of field has the camera to be set in order to be able to render the picture 400 pixels high and have the background sharp?

From example 2 it is known that the height of the panorama in spherical projection is 1,003 pixels. The formula has to be rearranged to solve AOF, then we get

400 px x 180° / 1'003 px = 72°.

Example 4:
We have a panorama in the vertical cross cube format with a width of 1,800 pixels and a height of 2,400 pixels.
(a) how high may the picture be rendered, if the vertical angle of field of the camera is set to 30° and still get a sharp background?
(b) to which vertical angle of view has the camera to be set to get a focused backdrop in the rendered picture that is 500 pixels high?

Only half the surface contains data, the other half is black. The surface of this projection is 1,800 x 2,400 = 4,320,000 square pixels, half of this is 2,160,000 square pixels. As in example 2, the square root of half of this is calculated to get the height of the panorama:

SQRT(2,160,000 / 2) = 1,039 pixels.
 

(a) 1'039 x 30 / 180 = 173 pixels.
 

(b) 500 px x 180° / 1'039 px = 87°

Conclusion

Panoramas are needed in huge formats to get the backdrop unblurred for large renders and small angle of field settings for the camera. Quite obviously, there is a reason why backgrounds in renders are often blurred.

Apart from the advantage of a blurred background that the scene can be rendered without depth of field, there is another advantage: one does not have to be overly careful when creating a panorama. In fact, programs for assembling HDRI panoramas and transforming them into different projections, have filters to blur the final panorama or an option to apply motion blur to it.

Most of the HDRI panorama projections that can be found on the Internet for downloading are already rather blurred. The small sphere – which seems to be some sort of mandatory in such renders – mirrors the HDRI focused well enough, because of its small size. An HDRI delivers interesting ambient light even if it is not being rendered as backdrop, though.