< 3D Welt
> Intro
• Korrektur
— 3D Welt: Spiegelkugel, Korrektur —
Sphärische Transformation und Korrektur
Programme, welche ein Panorama in eine interaktive Animation konvertieren, können mit der Aufnahme einer Spiegelkugel nichts anfangen. Um den von der Kugel verdeckten Teil der Umgebung zu ergänzen und auch um Fotograf und Kamera aus der Spiegelung zu entfernen, transformiert man die Abbildung auf der Kugel in eine andere Projektion. Folgende Namen für die hier interessierenden Projektion sind mir bis anhin begegnet:
-
Für die sphärische Projektion:
- Spärisch (spherical),
- Äquirektangulär (equirectangular)
- Länge/Breite (latitude/longitude {tatsächlich: Breite/Länge}),
- PSphere,
- Mercato, Mercator.
- Mirror Ball (Spiegelkugel),
- Konvexer Spiegel,
- Längentreue Azimuthalprojektion.
- Angular Map,
- Light Probe,
- Distanz Azimuthalprojektion.
Es ist die zylindrische Abwicklung einer Kugel auf eine Fläche, sie ist am Äquator flächentreu und gegen die Pole hin immer stärker verzerrt, der Pol – ein Punkt – wird zur Linie. Wir kennen diese Projektion von der Weltkarte. Trotz den beträchtlichen Verzerrungen zeigt sie die Kugeloberfläche auf eine verständliche Art.
Äquatoriale Sicht
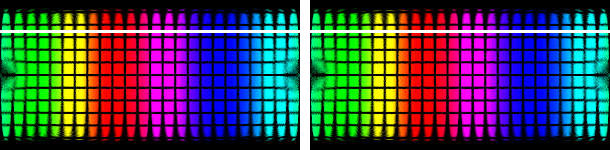
Die Aufnahmen von der Spiegelkugel wurden in die sphärische Projektion überführt. In dieser Projektion ist die hintere Seite der Kugel an den seitlichen Bildrändern abgebildet, die Pole oben und unten.
Im linken Bildteil die direkte Transformation, im rechten die korrigierte. Tatsächlich musste die 1° Aufnahme nicht korrigiert werden und die Bildteile sind identisch. Die weiße Linie ist als Orientierungshilfe eingezeichnet. Außer an der Stelle des Blinden Flecks und der stark komprimierten Spiegelung am Kugelrand sind keine Fehler erkennbar.
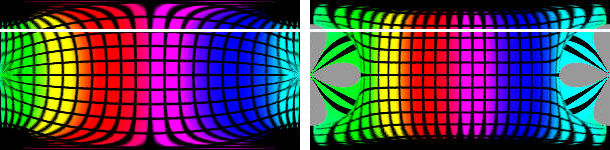
Schlimmer sieht es bei der 59° Aufnahme aus. Die Verzerrungen sind extrem, der fehlende Bildteil riesig.
Der linke Bildteil zeigt die unkorrigierte Transformation, der rechte die korrigierte. Bei diesen extremen Verzerrungen kann man natürlich keine Wunder erwarten, immerhin sind die Breitengrade in der Mitte waagrecht, wie die weiße Hilfslinie zeigt. Der nicht sichtbare Teil der Kugeloberfläche ist riesig, in der unkorrigierten Projektion erscheint er viel kleiner, als er tatsächlich ist.
Korrektur
Die Transformation von der Kugeloberfläche in eine planare, sphärische
Projektion gelingt nicht fehlerlos, weil ein Teil – der Blinde Fleck –
fehlt, das Transformationsprogramm aber davon ausgeht, dass die Kugeloberfläche
vollständig vorliegt. Die Korrektur bei der 59° Aufnahme bestand darin, den
fehlenden Bildinhalt zur Verfügung zu stellen. Im Bild oben rechts grau
dargestellt.
Die Aufnahme der Kugel wurde auf allen Seiten um die fehlende Anzahl Pixel ergänzt.
Man berechnet die Größe, die das Bild haben müsste, um die Kugel vollständig abzubilden. Dann erstellt man ein neues Bild in dieser Größe und kopiert die Aufnahme in dessen Mitte. Die Aufnahme ist quadratisch, die neue Kantenlänge berechnet man mit der Formel:
-
- S = s • 360 / (360 - 2 • arc sin(r / D))
- wobei:
S = neue Kantenlänge,
s = Kantenlänge der Aufnahme,
r = Radius der Spiegelkugel und
D = Distanz Kamera zum Mittelpunkt der Spiegelkugel;
arc sin = arcus sinus, inverse Sinusfunktion, sin-1,
360 = 360° Umfang.
Beispiel: r = 1 cm, D = 2.5 cm, s = 300 Pixel.
S = 300 x 360 / (360 - 2 x arc sin(1 / 2.5)) =
108'000 / (360 - 2 x arc sin(0.4)) =
108'000 / (360 - 2 x 23.578178) =
108'000 / (360 - 47.156357) =
108'000 / 312.84364 = 345.22038 = 345 Pixel.
Praxisnahes Beispiel: Kugeldurchmesser 2.5", Radius = 3.175 cm, Distanz Kamera zu Kugel = 94 cm, Bildgröße = 2'000 Pixel.
S = (2'000 x 360 / (360 - 2 x arc sin(3.175 / 94) =
720'000 / (360 - 2 x arc sin(0.0337765)) =
720'000 / (360 - 2 x 1.9356245) =
720'000 / (360 - 3.812491) =
720'000 / 356.12875 = 2'021.7407 = 2'022 Pixel.
Polare Sicht
Die Aufnahmen von der Spiegelkugel wurden in die sphärische Projektion überführt. In dieser Projektion ist die hintere Seite der Kugel am gegenüberliegenden Pol abgebildet, die Pole sind oben und unten.
Wird die Polare Sicht in die sphärische Projektion transformiert ergeben sich andrere Verzerrungen als bei der Äquatorialen. Die Ansicht ist ja auch um 90° gekippt. Folglich muss auch anders entzerrt werden.
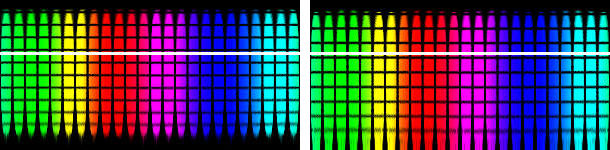
Der linke Bildteil zeigt die 1°, der rechte die 59° Aufnahme. Die weiße Linie dient als Orientierungshilfe. Man sieht, dass die Linien der Breitengrade nicht die gleichen Abstände voneinander haben.
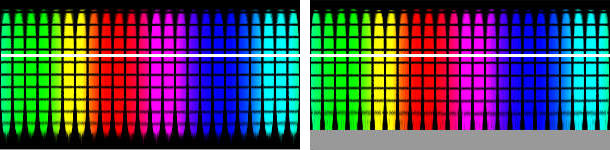
Die Projektionen wurden entzerrt. Links wieder die 1° und rechts die 59° Aufnahme. Die Abstände der horizontalen Linien ist gleich.
Korrektur
Die Transformation von der Kugeloberfläche in eine planare, sphärische
Projektion gelingt nicht fehlerlos, weil ein Teil – der Blinde Fleck –
fehlt, das Transformationsprogramm aber davon ausgeht, dass die Kugeloberfläche
vollständig vorliegt. Die Korrektur bestand darin, das zu hohe Bild zu verkleinern
und anschließend wieder ein Bild mit einem 2 : 1 Seitenverhätnis zu erstellen.
Im Bild oben rechts grau dargestellt is jener Teil, welcher ergänzt werden musste.
Bei der Transformation wird das quadratische Bild in eines mit dem Seitenverhältnis 2 : 1 gerechnet, entsprechend der 360° von links nach rechts und den 180° von oben nach unten. Der Blinde Fleck ist unten am Südpol der Kugel, wenn sie von oben fotografiert wurde. Je größer dieser Blinde Fleck ist, desto mehr wird das Bild durch die Transformation in die Länge gezogen.
Die kürzere Höhe des Bildes berechnet man mit der Formel:
-
- S = s • ((360 - 2 • arc sin(r / D)) / 360)
- wobei:
S = neue Kantenlänge,
s = Kantenlänge der Aufnahme,
r = Radius der Spiegelkugel und
D = Distanz Kamera zum Mittelpunkt der Spiegelkugel;
arc sin = arcus sinus, inverse Sinusfunktion, sin-1,
360 = 360° Umfang.
Beispiel: r = 1 cm, D = 2.5 cm, Bildgröße = 300 x 300 Pixel, nach der Transformation 300 x 150 Pixel (Breite x Höhe).
S = 150 x ((360 - 2 x arc sin(1 / 2.5)) / 360) =
150 x ((360 - 2 x arc sin(0.4)) / 360) =
150 x ((360 - 2 x 23.578178) / 360) =
150 x ((360 - 47.156357) / 360) =
150 x 312.84364 / 360 = 130.35152 = 130 Pixel.
Das Bild muss von 300 x 150 auf 300 x 130 skaliert werden, dann muss ein Streifen von 300 x 20 Pixel angefügt werden, damit das Bild wieder 300 x 150 Pixel wird.
Praxisnahes Beispiel: Kugeldurchmesser 2.5", Radius = 3.175 cm, Distanz Kamera zu Kugel = 94 cm, Bildgröße = 2'000 x 2'000 Pixel, nach der Transformation 2'500 x 1'250.
S = 1'250 x ((360 - 2 x arc sin(3.175 / 94)) / 360) =
1'250 x ((360 - 2 x arc sin(0.0337765)) / 360) =
1'250 x ((360 - 2 x 1.9356245) / 360) =
1'250 x ((360 - 3.8712491) / 360) =
1'250 x 356.12875 / 360 = 1'236.5582 = 1'237 Pixel.
Am Ende fehlt ein Streifen von 13 Pixel in der Höhe.
© 2004 - 2018 by Horo Wernli.