< Raytracing

< 3D World

> Intro

> Overview

> Distortions

• Correction

> Combining

— 3D World: Mirror Ball, Correction —

Transformation to Spherical and Correction

Programs that can convert a panorama into an interactive animation usually cannot handle a photograph of a mirror ball. To complement the part occluded by the sphere and to remove the photographer from the picture, the reflection on the sphere is transformed into another projection. I came across the following terms for the projections that concern us here:

For the spherical projection:

• spherical,
• equirectangular,
• latitude/longitude,
• PSphere,
• Mercato, Mercator.

For mirror balls:

• Mirror Ball,
• Convex Mirror,
• Azimuthal Equal Area.

For radial symetrical projections:

• Angular Map,
• Light Probe,
• Azimuthal Distance.

It is a cylindrical projection of a sphere on a flat surface, it is true to an area at the equator but gets increasingly distorted towards the poles. The pole — a point — becomes a horizontal line. We are familiar with this kind of projection from the world map. In spite of the considerable distortions, the surface of a sphere is shown in a comprehensive manner.

Equatorial View

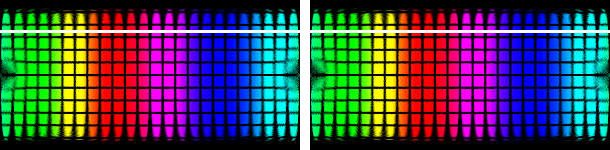
The photographs from the mirror ball were transformed into the spherical projection. In this projection, the back side of the sphere is depicted at the sides, the poles are on top and on the bottom.

The left part of the picture shows the direct transformation, the right part the corrected one. Actually there was no need for correction for the the 1° picture and both parts are identical. The white line was inserted as an aid. Except for the neighbourhood around the Blind Spot and the strongly compressed part from the edge of the sphere, there are no flaws visible.

It looks much worse for the 59° picture. The distortions are considerable, the missing part huge.

The left part of the picture shows the direct transformation, the right part the corrected one. We cannot expect wonders at this amount of distortion but at least in the centre, the longitude lines are straight as can be seen with the help of the white line. The invisible part of the sphere's surface is huge, it looks much smaller in the uncorrected projection than it actually is.

Equalisation
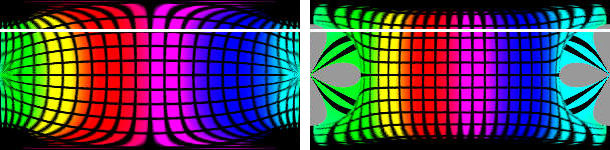
The transformation of the surface of a ball to a planar, spherical projection cannot be accomplished without deformations. The Blind Spot is missing (hence the name) and the transformation programm assumes it is fed the complete surface of a sphere. The correction of the 59° picture consisted of supplying the missing part of the image. This part is shown in grey in the picture above at right.

A frame around the picture of the sphere was added to supplement the missing number of pixels.

The size, the picture ought to have to show the full sphere is calculated. Then, a new picture is created with that size and the original picture is copied into its centre. The picture has a square aspect ratio, the new length of the edge can be calculated with this formula:

S = s • 360 / (360 - 2 • arc sin(r / D))

where:
S = new length of one side,
s = length of the original picture,
r = radius of the mirror ball, and
D = distance from the camera to the centre of the mirror ball;
arc sin = arcus sinus, inverse sine, sin^-1,
360 = 360° circumference.

Example: r = 1 inch, D = 2.5 inch, s = 300 pixel.

S = 300 x 360 / (360 - 2 x arc sin(1 / 2.5)) =
108'000 / (360 - 2 x arc sin(0.4)) =
108'000 / (360 - 2 x 23.578178) =
108'000 / (360 - 47.156357) =
108'000 / 312.84364 = 345.22038 = 345 pixel.

Real world example: diameter of mirror ball 2.5", radius = 1.25", distance camera to ball = 37", picture size = 2'000 pixel.

S = (2'000 x 360 / (360 - 2 x arc sin(1.25 / 37) =
720'000 / (360 - 2 x arc sin(0.0337837)) =
720'000 / (360 - 2 x 1.9360366) =
720'000 / (360 - 3.8720733) =
720'000 / 356.12793 = 2,021.7454 = 2,022 pixel./p>

Polar View

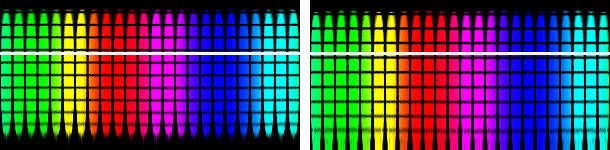
The photographs from the mirror ball were transformed into the spherical projection. In this projection, the back side of the sphere is depicted at the opposite pole, the poles are on top and on the bottom.

If the Polar View is transformed into the spherical projection, the distortions are different from those with the Equatorial View. The picture is tilted by 90°, so what did we expect? Therefore, it must also be equalised differently.

The left part of the picture shows the 1° image, the right one that from the 59° one. The white line is again an aid for the eye. As can be seen, the distances between the lines of equal latitude are different.

The projections were equalised. On the left half, again the 1° picture and the right part the 59° picture. The distances between the horizontal lines are the same.

Equalisation
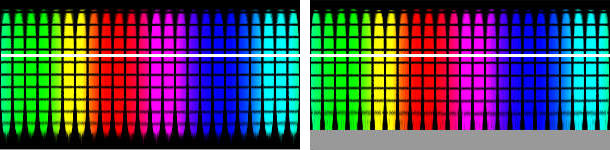
The transformation of the surface of a ball to a planar, spherical projection cannot be accomplished without deformations. The Blind Spot is missing and the transformation programm assumes it is fed the complete surface of a sphere. The picture was too high and was down scaled. Subsequently, a picture with an aspect ratio of 2 : 1 was created. The grey part in the picture above at right is the part that had to be inserted.

The transformation creates from the square aspect ratio picture a rectangular one with an aspect ratio of 2 : 1 according to the 360° from left to right and the 180° from top to bottom. The Blind Spot is below at the south pole of the sphere, if the ball was photographed from above. The larger this Blind Spot, the more the picture is stretched by the transformation.

The shorter hight can be calculated using this formula:

S = s • ((360 - 2 • arc sin(r / D)) / 360)

where:
S = new length of one side,
s = length of the original picture,
r = radius of the mirror ball, and
D = distance from the camera to the centre of the mirror ball;
arc sin = arcus sinus, inverse sine, sin^-1,
360 = 360° circumference.

Example: r = 1", D = 2.5", picture size = 300 x 300 pixel, after the transformation 300 x 150 pixel (width x height).

S = 150 x ((360 - 2 x arc sin(1 / 2.5)) / 360) =
150 x ((360 - 2 x arc sin(0.4)) / 360) =
150 x ((360 - 2 x 23.578178) / 360) =
150 x ((360 - 47.156357) / 360) =
150 x 312.84364 / 360 = 130.35152 = 130 pixel.

The picture has to be scaled from 300 x 150 to 300 x 130, a strip of 300 x 20 pixel has to be added to get the aspect ratio back to 2 : 1 (300 x 150 pixel).

Real world example: diameter of mirror ball 2.5", radius = 1.25", distance camera to ball = 37", picture size = 2,000 pixel, 2,500 x 1,250 pixel after the transformation.

S = 1'250 x ((360 - 2 x arc sin(1.25 / 37)) / 360) =
1,250 x ((360 - 2 x arc sin(0.0337837)) / 360) =
1,250 x ((360 - 2 x 1.9360366) / 360) =
1,250 x ((360 - 3.8720733) / 360) =
1,250 x 356.12793 / 360 = 1,236.5553 = 1,237 pixel.

There is a strip of 13 pixels missing to get to the correct hight.